Reasoning: Mental Models

Long, long ago, Richard asked how reasoning works. I don't think I've really answered that question in the first three posts responding to Richard's question, and this post isn't likely to either, but I hope I've provided some food for thought. In the first post, I talked about two types of reasoning errors that humans commonly make. In the second, I discussed the domain-general vs. domain-specific debate raised by research on one type of reasoning error. In the third, I talked about analogical reasoning and category-based induction. In this post, I'm going to describe mental models, and how they explain various types of reasoning. If you haven't guessed by now that my own view of reasoning is largely domain-general, this post should leave no doubt. Mental models treat domain-specific reasoning phenomena as products of domain-specific representations, rather than domain-specific reasoning mechanisms. This is, by and large, my own view as well. Mental models can be adapted to fit into traditional AI frameworks (though they differ from classical AI approaches in important ways, which will be described below) or more recent embodied cognition approaches (Lakoff's idealized cognitive models, for instance, are a form of mental models).

Mental models comprise what may be one of the most controversial and powerful theories of human cognition yet formulated. The basic idea is quite simple: thinking consists of the construction and use of models in the mind/brain that are structurally isomorphic to the situations they represent. This very simple idea, it turns out, can be used to explain a wide range of cognitive tasks, including deductive, inducitive (probabilistic), and modal reasoning. There are several ways of conceptualizing mental models, such as scripts or schemas, perceptual symbols, or diagrams. Here I am only going to deal with what mental model theories have in common in their treatments of human reasoning.

The idea that cognition uses mental models to think and reason is not a new one. "Picture theories" of thougth were common among the British empiricists of the 17th and 18th centuries, and were also held by many philosophers and psychologists in the first half of the 20th century (e.g., Wittgenstein's picture theory from the Tractatus). However, with the beginning of the cognitive revolution in the late 1950s and early 1960s, the computational metaphor of mind led to the prominence of propositional, or digital theories of representation and reasoning. Mental models returned to prominence in the 1980s because of their sheer predictive power. Study after study demonstrated that human reasoning exhibited certain features predicted by mental models, and not by propositional theories. Thus, for the last two decades, mental model theorists and propositional reasoning theorists have been locking horns and trading experimental arguments over how best to conceptualize human thought.

As I said before, the mental models view of mind is quite simple. For instance, the statement "The red square is above of the green circle" might be represented by the following mental model:

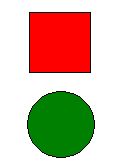
The model can be altered to fit any possible configuration. If the statement was more vague, we might construct several mental models to account for all of the possible interpretations. For instance, if the statement were "The red square is next to the green circle," we might construct multiple models with different "next-to" relationships, including one with the square to the right of the circle, one with it to the left, one with above, one with it below, and so on until all of the possible interpretations were represented. The difference between this representation and the propositional one¹ are straightforward. The propositional represents the structure of the situation without preserving that structure in the form of the representation, while the mental model represents that structure through an isomorphic structure in the representation.

One problem with the way I've described mental models thusfar is that it might be tempting to see mental models synonymous with perceptual (particularly visual) imagery. However, not all mental models are perceptual images, and research has shown that perceptual imagery itself may be built on top of mental models. In addition, mental models can represent abstract concepts that may not be visualizable, such as "justice" or "good." The important aspect of mental models is not that they are or are not perceptual, but that they preserve the structure of the situations they represent, which can be done with perceptual images or non-perceptual representations.

To see how mental models work in reasoning, I'm going to describe mental model theories of three different types of reasoning: deductive/syllogistic, probabilistic, and modal. For each type of reasoning, mental model theories make unique predictions about the types of errors people will make. Hopefully by the end, even if you don't agree with the mental models perspective, the research on reasoning errors will have provided you with some new insights into the way the human mind works.

Deductive Reasoning

Recall the description of participants' performance in the Wason selection task from the first post. For the part of the solution that is identical with modus ponens participants answered successfully, but not for the part of the solution identical with modus tollens. According to propositional theories of reasoning, the best explanation for this is that people are in fact using modus ponens, or an equivalent rule, but not modus tollens. The mental models explanation differs in that it doesn't posit the use (or failure to use) either rule. Instead, people construct mental models of the situation, and use those to draw their conclusions. Here is how it works. Participants build a model of the premise(s) based on their background knowledge, and then come up with conclusions based on that model. To determine whether these conclusions are true, they check to see if they can construct any models in which it does not hold. If a conclusion holds in all of the models a person construct, then it is true. If not, then it is false.

In the Wason selection task, the problem is to determine which models result in the rule being true, and which result in it being false, and use this knowledge to decide which cards to turn over. In the version of the Wason task from the first post, the rule was, "If there is a vowel on one side of a card, then there is an odd number on the other side," and we had these cards:

There are various models in which this rule is true. They are the following:

VOWEL ODD

CONSONANT EVEN

CONSONANT ODD

ODD VOWEL

ODD CONSONANT

EVEN CONSONANT

However, only the first of these explicitly represents the elements mentioned in the rule, and given working memory restrictions, we're likely to only use the elements in the first model when testing the rule. If there is a vowel (e.g., E) on the visible side of a card, then there are two possibilities for the other side. In a mental model, they would be represented with the following:

ODD

EVEN

In some models (the ones with ODD on the other side) the rule is true, and in some (the ones with EVEN) it is false. Thus, the person knows that he or she must turn the card with the vowel over to test the rule. However, due to working memory constraints, we tend to consider only a small number of alternative models, and thus we're only likely to represent models that contain elements from our mental model of the rule. Since there is no EVEN in our model of the rule, we're unlikely to think that we need to turn over the card with the 2 showing, and because there is an ODD in the rule model, we are likely to mistakenly think that we need to turn over the 7. Things are actually a little bit more complex than this. It turns out that representing negations in situations like this (where the content of the models if fairly abstract or unfamiliar) is more difficult (because it requires the construction of more mental models) than representing positive situations, but for our purposes, it suffices to say that working memory makes it less likely to consider models that aren't easily derived from our model of the rule.

To see better how this works, consider the following problems from Johnson-Laird et al. (1998)²:

Only one of the following premises is true about a particular hand of cards:

There is a king in the hand or there is an ace, or both.

There is a queen in the hand or there is an ace, or both.

There is a jack in the hand or there is a 10, or both.

Is it possible that there is an ace in the hand?

Johnson-Laird et al. give the following explantion of participants' performance on this sort of problem:

For problem 1, the model theory postulates that individuals consider the true possibilities for each of the three premises. For the first premise, they consider three models, shown here on separate lines, which each correspond to a possibility given the truth of the premise:

king

ace

king ace

Two of the models show that an ace is possible. Hence, reasoners should respond, "yes, it is possible for an ace to be in the hand". The second premise also supports the same conclusion. In fact, reasoners are failing to take into account that when, say, the first premise is true, the second premise:

There is a queen in the hand or there is an ace, or both

is false, and so there cannot be an ace in the hand. The conclusion is therefore a fallacy. Indeed, if there were an ace in the hand, then two of the premises would be true, contrary to the rubric that only one of them is true. The same strategy, however, will yield a correct response to a control problem in which only one premise refers to an ace. Problem 1 is an illusion of possibility: reasoners infer wrongly that a card is possible. A similar problem to which reasoners should respond "no" and thereby commit an illusion of impossibility can be created by replacing the two occurrences of "there is an ace" in problem 1 above with, "there is not an ace". (emphasis in the original)

Here is another example from Johnson-Laird, et al. (1998):

Suppose you know the following about a particular hand of cards:

If there is a jack in the hand then there is a king in the hand, or else if there isn’t a jack in the hand then there is a king in the hand.

There is a jack in the hand.

What, if anything, follows?

For which they give this explanation:

Nearly everyone infers that there is a king in the hand, which is the conclusion predicted by the mental models of the premises. This problem tricked the first author in the output of his computer program implementing the model theory. He thought at first that there was a bug in the program when his conclusion -- that there is a king -- failed to tally with the one supported by the fully explicit models. The program was right. The conclusion is a fallacy granted a disjunction, exclusive or inclusive, between the two conditional assertions. The disjunction entails that one or other of the two conditionals could be false. If, say, the first conditional is false, then there need not be a king in the hand even though there is a jack. And so the inference that there is a king is invalid: the conclusion could be false.

The take-home lesson from all of this is that in deductive problems, working memory constraints that cause us to consider a limited number of mental models lead us to make systematic errors in reasoning, including those found in the original Wason selection task. It also explains why, when we place the Wason task in a familiar context (e.g., alcohol drinkers and age), we perform better. For these scenarios, we already have more complex mental models in memory, and can use these, rather than models constructed on-line for the specific task, to reason about which cards to turn over.

Probabilistic Reasoning

Reasoning about probabilities occurs in a way that is very similar to deductive reasoning. The mental models view of probabilistic reasoning has three principles: 1.) people will construct models representing what is true about the situations, according to their knowledge of them 2.) all things being equal (i.e., unless we have some reason to believe otherwise), all mental models are equally prob2bly, and 3.) the probability of any situation is determined by the proportion of the mental models in which it occurs³. If an event occurs in four out of six of the mental models i construct for a situation, then the probability of that event is 67%. However, because mental models are subject to working memory restrictions, they will lead to certain types of systematic reasoning errors in probabilistic reasoning, as they do in deductive reasoning. For instance, consider this problem ⁴:

On my blog, I will post about politics, or if I don't post about politics, I will post about both cognitive science and anthropology, but I won't post all on three topics.

For this scenario, the following mental models will be constructed:

POLITICS
COG SCI ANTHRO

What is the probability that I will post about politics and anthropology? If all possibilities are equally likely, the answer is 1/4. However, researchers found that in problems like this, people tend to answer 0. The reason for this is that in the two mental models people construct for this situation, there is no combination of politics and anthropology.

Another interesting and widely-studied example is the famous Monty Hall problem. For those of you who haven't heard of it, I'll briefly describe it, and then discuss it from a mental models perspective. On the popular game show Let's Make a Deal, hosted by Monty Hall, people were sometimes presented with a difficult decision. There were three doors, behind one of which was a great prize. The other two had lesser prizes behind them. After people made their first choice, Hall would open one of the doors with a lesser prize, and ask them if they wanted to stick with their choice, or choose the remaining door. The question is, what should participants do? Does it matter whether you switch or stay with your original choice? If you're not familiar with the problem, think about it for a minute, and come with an aswer before reading on.

Do you have an answer? If you're not familiar with the problem, the chances are you decided that it doesn't matter whether you switch. However, if this is your answer, then you are wrong. The probability of selecting the door with the big prize, if you stick with your original choice, is 33%. The probability of selecting the door with the big prize if you switch, however, it 66.6%. To see why this is, imagine another situation, in which there are a million doors to choose from. You choose a door, and Monty then opens 999,998 doors, leaving one more, and asks you if you want to choose? In this situation, it's quite clear that while the chance of selecting the right door on the first choice was 1/1,000,000, the chance of the remaining door being the right one are 999,999/1,000,000.

When participants have been given this problem in experiments, 80-90% of them say that there is no benefit to switching. They believe that the probability of the remaining door containing the big prize is no greater than the probability of the door they've already chosen containing it (the so-called "uniformity belief")⁵. In general they either report that the number of original cases determines the probability of success (probability = 1/N), so that the probability in the first choice is 1/3, and in the second choice it is 1/2, or they believe that the probability of success remains constant for each choice even when one is eliminated⁶. Recall the three principles of the mental models theory of probabilistic reasoning. According to these, people will first construct mental models of what they know about the situation. In the Monty Hall problem, they will construct these three models:

DOOR 1 BIG PRIZE
DOOR 2 BIG PRIZE
DOOR 3 BIG PRIZE

Each of these models is assumed to be equally probably, and the probability of any one of the models being true is 1 over the total number of models, or 1/3. After the first choice has been made, and one of the other doors eliminated, people either use this original model, in which case they assume that the probability of the first door chosen and the remaining door are both 1/3, or they construct a new mental model with the two doors, and thus reason that the probability for both doors is 50%. Their failure to represent the right number of equipossible models, and therefore reasoning correctly, is likely due to working memory straights, and research has shown that by manipulating the working memory load of the Monty Hall problem, you can get better or worse performance⁷.

Modal Reasoning

The mental models account of modal reasoning should be obvious, from the preceding. To determine whether a state of affairs is necessary, possible, or not possible, one simply has to construct all of the possible mental models, and determine whether the state of affairs occurs in all (necessary), some (possible) , or none (not possible) of the models. There hasn't been a lot of research on modal reasoning using mental models, because it is similar to probabilistic reasoning, but people's modal reasoning behaviors do seem to be consistent with the predictions of mental models theories.In particular, people seem to make assumptions of necessity or impossibility that are incorrect, due to the limited number of mental models that they construct (e.g., in Johnson-Laird et al. (1998)'s first problem described in the section on deductive reasoning).

So, that's reasoning. There are all sorts of phenomena that I haven't talked about, and maybe I'll get to them some day, but for now, I'm going to leave the topic of reasoning. I hope Richard is at least partially satisfied, and maybe someone else has enjoyed these posts as well. If anyone has any further requests, let me know, and I'll post about them if I can.


¹ There are various ways of describing propositional representations. A common way of representing the sentence "The redsquare is above the green circle" is ABOVE(RED(SQUARE),GREEN(CIRCLE)).
² Johnson-Laird, P. N., Girotto, V., & Legrenzi, P. (1998). Mental models: a gentle guide for outsiders.
³ Johnson-Laird, P.N., Legrenzi, P., Girotto, V., Legrenzi, M.S., & Caverni, J.P. (1999). Naive probability: a mental model theory of extensional reasoning. Psychological Review, 109(4), 722-728.
⁴ Adapted from Johnson-Laird, et al (1999).
⁵ See, e.g., Granberg, D., & Brown, T. A. (1995). The Monty Hall dilemma. Personality and Social Psychology Bulletin, 21, 711–723; Falk, R. (1992). A closer look at the probabilities of the notorious three prisoners. Cognition, 43, 197–223.
⁶ Shimojo, S., & Ichikawa, S. (1989). Intuitive reasoning about probability: Theoretical and experimental analyses of the “problem of three prisoners.” Cognition, 32, 1–24.
⁷ Ben-Zeev, T., Dennis, M, Stibel, J. M., & Sloman, S. A. (2000). Increasing working memory demands improves probabilistic choice but not judgment on the Monty Hall Dilemma. Paper submitted for publication.